
�������̃g�s�b�N�X�Q�O�P�O�i�y��ҁj��
�E�h�����̃g�s�b�N�X�i�y��ҁj�h�́A�y��Ɋւ��钍�ڂ��ׂ��b����v���܂܂ɏ����Ă݂悤�Ƃ����R�[�i�[�ł��B�����݂Ȃ���̎Q�l�ɂȂ�Ǝv���Ă���܂��B�@�i���A�뎚�^�E����A��������e�^�D�܂����Ȃ����e������������ꂽ�ꍇ�ɂ́A�f�薳���C�����邱�Ƃ�����܂��̂ŁA�䗹�����������B�j
���ڎ���
�i�P�����j�@�����p�I�ɉ��y���_���w�ڂ��i��U��F�x���ɂ�鉹���\�L�̘b�i���̂P�j�j��
�i�Q�����j�@�����p�I�ɉ��y���_���w�ڂ��i��V��F�x���ɂ�鉹���\�L�̘b�i���̂Q�j�j��
�i�R�����j�@�����p�I�ɉ��y���_���w�ڂ��i��W��F�x���ɂ�鉹���\�L�̘b�i���̂R�j�j��
�i�S�����j�@�����p�I�ɉ��y���_���w�ڂ��i��X��F�x���ɂ�鉹���\�L�̘b�i���̂S�j�j��
�i�T�����j�@�����p�I�ɉ��y���_���w�ڂ��i��P�O��F�x���ɂ�鉹���\�L�̘b�i���̂T�j�j��
�i�Q�O�P�O�N�@�P�����j
�����p�I�ɉ��y���_���w�ڂ��i��U��F�x���ɂ�鉹���\�L�̘b�i���̂P�j��
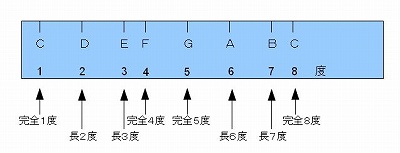
�@�Q�O�P�O�N�̑�P��ڂ́A���y���_�̐��E�ɂ����ẮA��ʂ̂����ɂƂ��čł��ǂɂȂ�ł��낤�u�x���v�ɂ�鉹���\�L�̘b���ł��B
�@�u�x���𗝉����A�g�����Ȃ���悤�ɂȂ�A���͂≹�y���_�̐��E�Ɋ���e���߂��̂����R�v�ƌ�����قǁA���̕����͑S�ẴJ�M�ƂȂ�悤�Ȃ��̂ł���܂��B
�@����Ɋւ��Ă��A�Ȃ�ׂ����S�҂̂����ɂƂ��Ă킩��₷���悤�ɏ����Ă݂܂��̂ŁA�u���܂�J�^�C���Ƃ͌��������i�V�v�Ƃ������ƂŁA���肢�ł���Ǝv���܂��B
�@�Ƃ͌����A��͂�A���̍��ڂ͈�Ԃ̓�ւƌ����Ă��ǂ����́B�@�������b����i�߂Ă������Ƃɂ��܂��傤�B
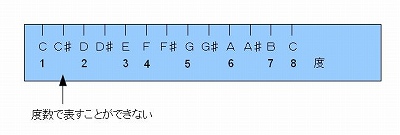
�U�|�P�D�x���Ƃ͉��H
�@�u�Q�̉��̊Ԃ̊u����̑傫���v�̂��Ƃ������i�C���^�[�o���j�ƌĂт܂��B
�@�x���Ƃ́A���̉�����\���ۂ̒P�ʂł��B
�@���Ȃ킿�A���������ڂ��������A�C�ӂ̂Q�̉������݂��A�Е��̉�����Ƃ����ꍇ�̂�������̉��܂ł̉��y�I�ȋ������u�����v�ł����āA�����\�L����ۂ̒P�ʂ��u�x�v�ł���Ƃ������Ƃł��B
�@��X�̓���̐��E�ł́A�Q�̓_�i�Q�̕����j�̊Ԃ̒����𑪂낤�Ƃ���ꍇ�AFig �U�|�P�|�P�̂悤�ɁA�ڐ���̕t������K�i�������j���g���A����̓_�ɒ�K�̌��_�āA��������̈ʒu���`cm�̖ڐ���ʒu�ɂȂ邩�H�Ŕ��f����A�Ƃ������Ƃ��s���܂��B
�@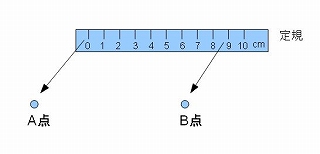
�@�@�e�����D�U�|�P�|�P�@�@�Q�_�Ԃ��K�ő���@
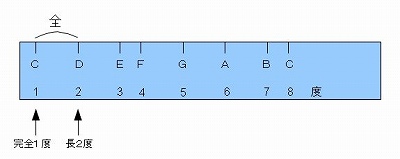
�@���y�̐��E�ł��A���l�Ȃ��Ƃ��s�����Ƃ��\�ł��B
�@�܂�A�Q�̉�������ꍇ�A���̊Ԃ��A���y�I�ȋ����Ƃ��Ăǂꂭ�炢����Ă��邩�H�𑪂邱�Ƃ��ł���Ƃ������Ƃł��B
�@����ɂ����ẮAFig �U�|�P�|�Q�̂悤�ɁA���y�̐��E�ɂ������K�����݂��A������g���āA�Q�̉��Ԃ̋����𑪂邱�ƂɂȂ��Ă��܂��B
�@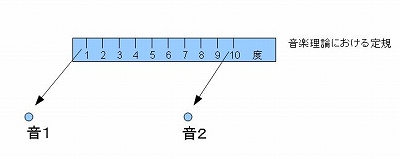
�@�@�e�����D�U�|�P�|�Q�@�@���y�̐��E�ł��A�Q�̉��̊Ԃ��K�ő����@
�@�����ŁA���̂悤�Ȃ��Ƃ�ǂ�ł����ƁA�u���̊Ԃ̋����𑪂����肵�āA���̂��߂ɂȂ�̂��H�v�Ǝv����������܂���B
�@�������A���́u���y�I�����v�̍l�������w��ł����A�u�a���i�R�[�h�j�̖��̂f����ꍇ�v�A�u�w��Ŏ����ŃR�[�h�t�H�[�������ꍇ�v�A�܂��A�u���W���[�X�P�[���^�i�`�������}�C�i�[�X�P�[���ȊO�̊e��̃X�P�[�����������ĉ��t�Ɏg���ꍇ�v�A�Ȃǂɂ����āA�����ւ�֗��Ȃ��ƂɂȂ���̂Ȃ̂ł��B
�@�]���܂��āA���ꖳ�����ẮA���y���_�͌��Ȃ����̂Ȃ̂ł��B
�U�|�Q�D��K�͂b���W���[�X�P�[��
�@���̉��y�i���y���_�j�̐��E�ɂ������K�̐��̂Ƃ́A���́A�h���~�t�@�\���V�h�A���Ȃ킿�A���Ȃ��݂̂b���W���[�X�P�[���ł��B�i�˂���ς�A�����ł��b���W���[�X�P�[�����厖�Ƃ������Ƃł���܂��ˁB�j
�@����āA�b���W���[�X�P�[���Ƃ�����K�̗l�q���܂��͒m��ׂ��A�Ƃ������ƂɂȂ�܂����A���������ڂ��������A�u���̒�K�̊e�ڐ���ɏ����Ă��鐔���i�x���j���悭�m���Ă����K�v������v�Ƃ��������ł��傤���B
�@�܂��́A�b���W���[�X�P�[���̉��ɏ��Ԃɔԍ������܂��ƁAFig �U�|�Q�|�P�̂悤�ɂȂ�܂����A���ꂪ�e�x���̔��������i�H�j�ƍl���Ă���������Ηǂ��ł��B
�@�u�b���P�x�̉��v�A�u�c���Q�x�̉��v�Ƃ��������ƂɂȂ�܂����A�u�P�܂���i�I�N�^�[�u��j�̂b�̉����W�x�Ɛ����邱�Ɓv�́A��ŏd�v�ȃ|�C���g�ƂȂ�܂��B�i������ƕs�v�c�Ȃ��Ƃł����E�E�j
�@
�@�@�e���� �U�|�Q�|�P�D�@�b���W���[�X�P�[���̉��ɔԍ���t����@
�@�܂�A���y�̐��E�ɂ́A����Fig �U�|�Q�|�Q�̂悤�Ȓ�K�����݂��A����ĂāA�Q�̉��̊Ԃ́i���y�I�j�����𑪂�Ηǂ��ƍl����킯�ł��B
�@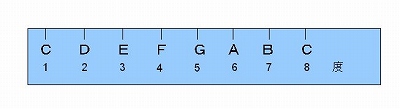
�@�@�e���� �U�|�Q�|�Q�D�@�b���W���[�X�P�[�������Ƃɂ������y�i���_�j�̐��E�ł̒�K�@
�@���̂悤�ɁA�e�����̕����ɖڐ��肪�ӂ��Ă����K�ƍl����̂ł����A��L�̃I�N�^�[�u��̂b���W�x�Ɛ����邱�Ƃɉ����A�܂����≹�y���_�̐��E�Ȃ�ł͂̕s�v�c�Ȍ��ۂ��������Ă��邱�Ƃɂ͒��ӂł��B
�@��X�������̐��E�Ŏg����K�̖ڐ���ɂ����錴�_�i�[�_�j�́A�Omm��A�O�����ł��B�@�������A���y���_�̐��E�̒�K�ɂ͂O�x�i�[���x�j�Ƃ������̂͑��݂��܂���B
�@���_�́A�O�x�ł͖����A�P�x�Ƃ������ƂɂȂ��Ă��܂��B
�@�߂�ǂ��Ȃ��Ƃł����A���傢�ƃK�}�����āA�u���̂悤�Ȏ����ł����āA�d�����Ȃ��B�v�Ǝ���܂��傤�B
�@����Ă����A���̊Ԃɂ���R�͖����Ȃ���̂ł��B
�U�|�R�D�������A����������Y��Ă͂Ȃ�Ȃ�
�@�������A�܂��l�����Ă������Ƃ�����܂��B
�@���ɂ��Ȃ��݂ƂȂ����ł��傤���A���}Fig �U�|�R�|�P�̂悤�ɁA�b���W���[�X�P�[���̊e���́A�S�|�S�|���|�S�|�S�|�S�|���ŕ���ł���܂�����A�S�����̕����ɂ́A����ɔ������ŕ�����ꂽ�������݂��Ă��܂��B
�@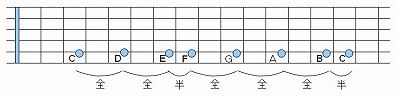
�@�@�e���� �U�|�R�|�P�D�@�b���W���[�X�P�[���̊e���̉����@
�@����āA�������l�����āA���y�i���_�j�̐��E�̒�K����萳�m�ɏ������Ƃ��Ă��AFig �U�|�R�|�Q�̂悤�ɁA�b��i�c��j��c��i�d��j�Ƃ��������̓x�������s���ƂȂ��Ă��܂����ƂɂȂ�܂��B
�@
�@�@�e���� �U�|�R�|�Q�D�@���������̖ڐ���̓x�������Ȃ��@
�@�Ƃ������ƂŁA���̌����Ă��镔���ɂ��A���炩�̕��@�Ŗ��̂�t���Ȃ��Ă͂Ȃ�܂���B
�@�����œo�ꂷ��̂��A�u���S�P�x�v�Ƃ��A�u���R�x�v�Ƃ��������̂ł��Ȃ��݂́A�u���S�v�A�u���v�A�u���v�A�u���v�A�u�Z�v�Ƃ������A�x���̐����̑O�ɕt�����ƂɂȂ�L���̂悤�ȁi�H�j���t�ł��B
�@���ꂪ�o�Ă���ƁA�܂������C�Ɍ��C�������Ȃ�A�����o�������Ȃ�l���������Ǝv���܂����A��{����������������A�ӊO�ƊȒP�ȊT�O�ł��B
�@����́A�����������Ă����܂��傤�B
�ˈȉ��A����ɑ���
�i�Q�O�P�O�N�@�Q�����j
�����p�I�ɉ��y���_���w�ڂ��i��V��F�x���ɂ�鉹���\�L�̘b�i���̂Q�j��
�@����́A�O��ɂ����āu���y���_�̐��E�ł̒�K�v�ƕ\���������m�ɂ��ẮA����Ȃ�����ƂȂ�܂����A�܂��́A����܂���ʂ̉���Ƃ͈قȂ�A�v���[�`���Ƃ�܂��傤�B
�@�V�|�P�D�x���̓Y�������̉p�ꖼ�́H
�@���Ɍ䑶�m�̂������������Ǝv���܂����A���̒�K�ɂ�����ڐ���̖��̂ɕt���Ă�����̂́A�u���S�v���u���v���u���v���A�����āA�u���v���u�Z�v���A�������킩��ɂ������t����ƂȂ�܂��B
�@�������A�����̌��t�̉p�ꖼ������A���������킩��₷���Ȃ邩������܂���B
�@���S�� perfect
�@���� major
�@�Z�� minor
�@���� augmented
�@���� diminished
�@�܂��A�u���S�v�̉p�ꖼ�hperfect�h���ĉ��Ȃ́H�Ƃ��������ł��傤���A���Ȃ��Ƃ��A�u���v�Ɓu�Z�v�̓s���Ƃ���̂ł͂Ȃ��ł��傤���H
�@�����A�u���v�Ƃ́hmajor�h�A�v�́u�����v�́u���v�Ȃ킯�ł��B�i�����悤�ɁA�u�Z�v�Ƃ́hminor�h�ŁA�u�Z���v�́u�Z�v�B�j
�@����āA�u���v���t�����̂́A���W���[�X�P�[����W���[�̃R�[�h�ɊW���鉹�ɂȂ�̂��ȁH�Ƃ��A�u�Z�v���t�����̂́A�}�C�i�[�X�P�[����}�C�i�[�R�[�h�Ɋւ��̂��鉹�ɂȂ��Ă���̂��ȁH�Ƃ��A�z�����ł��邩�Ǝv���܂��B
�@���ƁA�haugmented�h�́A�haug�h�Ƃ����������t���I�[�M�������g�̃R�[�h�ɊW������́A�hdiminished�h�́A�hdim�h�����f�B�~�j�b�V���̃R�[�h�̊W���ȁH�A�Ȃ�Ă������Ƃɂ��C�Â��ł��傤�B
�@�V�|�Q�D�܂��͂P�x�ƂQ�x�̖��̂���
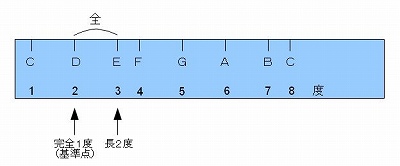
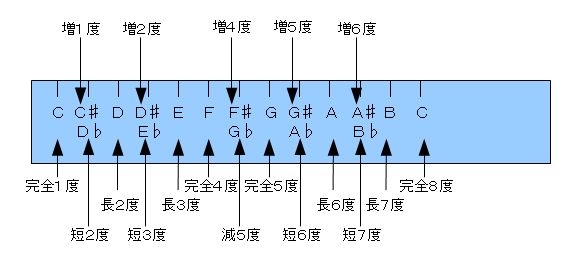
�@�ŏ��ɁA��K��̖ڐ�����A�b���W���[�X�P�[���̉��݂̂Ƃ��Ă݂܂��āA�b�Ƃc�̂Q�̉��ɂ��āA���Ă݂܂��B�i�e�����D�V�|�Q�|�P�Q�Ɓj
�@�O��܂łɂ����������悤�ɁA���̒�K�̌��_�͂b�̉��̈ʒu�ŁA���̖ڐ���̖��̂́u�O�x�v�ł͂Ȃ��A�u�P�x�v�ł���킯�ł����A���m�ɕ\���Ɓu���S�P�x�v�Ƃ������̂̂��̂ɂȂ�܂��B
�@�p��\�L�ł́A�hperfect 1st�h �ł����A�ʏ�́h1st�h�Ə����Ί��S�P�x�̈Ӗ��ɂȂ���̂ł��B
�@�u���S�v�Ƃ������t�̈Ӗ��́A�܂��C�ɂ��Ȃ��ł��������B�i�j
�@
�@�@�e�����D�V�|�Q�|�P�@�@���S�P�x�ƒ��Q�x�@
�@���ɂc�ł����A�c�̖ڐ���ʒu�́A���̒�K�Ƃ��Ă̘b�ł�����A�����܂ł��A�b�̈ʒu�����_�i��j�Ƃ����ꍇ�ɁA�S���P�������ꂽ�ʒu�Ƃ��������ƂȂ�܂��B
�@���̏ꍇ�̂c�̈ʒu���u���Q�x�v�ƌĂт܂��B�i�Ƃ肠�����́A���W���[�X�P�[����̉�������A�u���imajor�j�v�ł���ƈӎ����܂��傤�B
�@�p��\�L�ł́A�hmajor 2nd �h�A�ʏ�́A�h2nd �h��ok�ł��B
�@��薾�m�Ɍ����A�u�b����Ƃ������ɁA�b�Ƃc�͒��Q�x�̉����W�ɂ���v�Ƃ������ƂɂȂ�܂��B
�@�����ł̒��ӓ_�́A�b�Ƃc�́A�����܂ł��A���́A�h�b���W���[�X�P�[���𗘗p�������y�I�Ȓ�K�̖ڐ����̘b�h�ł����āA�b�Ƃc�̃y�A�������A�u���Q�x�v�̉������`������킯�ł͂Ȃ��Ƃ������Ƃł��B
�@���Ȃ킿�A�u���Q�x�v�Ƃ́A�����܂ł��A�P�S�����ꂽ�Q�̉��̋����i�����j�̖��̂ł��B������A�Ⴆ�A�c����ɂ����ꍇ�́A�d���u���Q�x�v�̉����W�ɂ���Ƃ�������킯�ł��B
�@�Ƃɂ����A���̂b�Ƃc�́A��K����������ł̊�{�I�Șb�ł��B�i�e�����D�V�|�Q�|�Q�Q�Ɓj
�@
�@�@�e�����D�V�|�Q�|�Q�@�@�c��ł̒��Q�x�@
�@�V�|�R�D�b�Ƃc�̊Ԃ̔��������́H
�@���悢��A�b�Ƃc�̊Ԃ̔��������̖ڐ���̖��̂������܂��傤�B�i�e�����D�V�|�R�|�P�Q�Ɓj
�@�܂��A���̂b��Ƃc��̂悤�ɁA���ۂ̉��͓����ł����̂��قȂ鉹�̃y�A�̂��Ƃ��u�ٖ������v�ƌĂсA�����Əd�v�Ȍ��ƂȂ��Ă��܂��B
�@�����āA���ɒ������鉹�͓����ł����̂��قȂ�Ƃ������Ƃł�����A�ڐ���̖��̂��قȂ��Ă���킯�ł��B
�@���̍ۂ̍ő�̃|�C���g�́A�h����ɂ���āA���Ƃ��Ɖ��ł����������ω��������H�h�Ƃ������Ƃł��B
�@�Ⴆ�A�b��Ƃ́A�b�Ƃ������Ɂt���Ĕ����オ�������̂ł�����A�b��̖��̂��A���S�P�x�̕ω��`�Ƃ��ĕ\���܂��B�@�v�́A�P�x�Ƃ��������͓����܂܂ŁA�u�`�P�x�v�ƕ\���A�Ƃ����b�Ȃ̂ł��B
�@�Ƃ������ƂŁA�u���S�P�x�v�ł���b�̔�����̂b��̖��̂́A�u���P�x�v�Ƃ������̂ɂȂ�܂��B
�@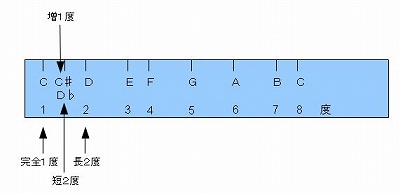
�@�@�e�����D�V�|�R�|�P�@�@���P�x�ƒZ�Q�x�@
�@�������c��́A�u���Q�x�v�ł���c�̕ω��`�i�c�����������������́j�ŕ\���A�u�Z�Q�x�@�i��2nd�j�v�ƂȂ�܂��B
�@�u�ٖ��������A�ǂ̂悤�ȏꍇ�ɗL���ɂȂ邩�H�v�A�܂��A��L�ɂ����āA�u�b��Ƃc��̂ǂ����I�ׂΗǂ����H�v���ɂ��ẮA����ȍ~�Ő����������܂����A�܂��́A���̋�ʂ́A�h�R�[�h�̎�ނ����肷���ŏd�v�ɂȂ�h�Ƃ��������ƂłƂ炦�Ă����Ă��������B
�@�V�|�S�D�ω����̂̋K�����o����ΑS�Ă���
�@�V�|�P���ł������܂����悤�ɁA�u���v�Ƃ́hmajor�h�̂��ƂŁA���W���[�X�P�[����̉��ɂ��傢�ɊW�����邱�ƂɂȂ�܂��B
�@�]���܂��āA�܂��͂����ŁA���W���[�X�P�[����̉��́i�ڐ���́j���̂�S�ď����Ă��܂��܂��ƁA�ȉ��̂e�����D�V�|�S�|�P�̂悤�ɂȂ�܂��B
�@
�@�@�e�����D�V�|�S�|�P�@�@���W���[�X�P�[����̊e���̖ڐ��薼�́@
�@�v�́A���W���[�X�P�[����ɂ́A�u���S�`�x�v�ƁA�u���`�x�v�̂Q�킵�����݂��Ȃ��킯�ł��B
�@����āA�����Ɂ��t���āA�����オ�����艺�������肵���ʒu�̂��̂��A���̑��̉��̈ʒu�ƂȂ���̂ł��B
�@�h���S�́A�P�@�S�@�T�@�W�h�Ȃ�Ă����悤�Ɋo���Ă��܂��Ă��ǂ��ł��傤�B�i�c��́A���Ǝv���Ηǂ��킯�ł��B�j
�@����ɂ����ẮA��q�����悤�ɁA�u���S�P�x�v�̔�����́u���P�x�v�A���Q�x�̔������́u�Z�Q�x�v�ȂǂƂȂ�̂ł����A�������������̂��̂ɂȂ��Ă��A�����̕ω����̂͌��܂������̂ƂȂ�܂��B
�@���������āA�������w�ŕ\�����A�ȉ��̕\�̂悤�Ȃ��̂��o����A�S�Ă̖ڐ���ʒu�̓x���̖��̂͒����ɕ������Ă��܂����ƂɂȂ�킯�ł��B
�@
�@�@�\�V�|�S�|�P�@���̕ω��̗l�q�@
�@�Ƃ������ƂŁA������e�����D�V�|�S�|�P�̂��ꂼ��̖��̂ɓK�p����A�ٖ��������܂߁A�ȉ��̂悤�ɔ����������\���邱�ƂɂȂ�܂��B�i�e�����D�V�|�S�|�Q�j
�@
�@�@�e�����D�V�|�S�|�Q�@�@�����P�ʂł̊e���̖ڐ��薼�́@
�@����ŁA���y���_�̐��E�ł̒�K�̗l�q���قڂ킩���Ă������ƂɂȂ�킯�ł��B
�@����́A��K�̗l�q�̒lj������A���тɁA�����x���\�L�̎g�����ł̒��ӎ����������������Ǝv���܂��B
�@�ˁ@�ȉ��A����ɑ���
�i�Q�O�P�O�N�@�R�����j
�����p�I�ɉ��y���_���w�ڂ��i��W��F�x���ɂ�鉹���\�L�̘b�i���̂R�j��
�@����́A�������Ȃ��݂ƂȂ����ł��낤�A���y�̐��E�̒�K�̗l�q�̒lj������A���тɁA�����x���\�L�̎g�����ł̒��ӎ����������܂��B
�@�v�́A��K�̎��ۂ̎g�����Ƃ��������Ƃł��B
�W�|�P�D�܂��܂�����ٖ������I
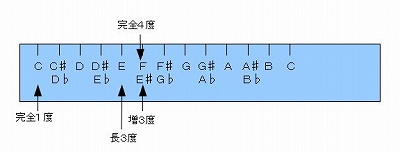
�@�O��A���Ƃ��Ă͓����ł����O���قȂ�u�ٖ������v�Ƃ������̂����グ�A�x���ɂ�鉹���\�L�ɂ����ẮA�u�ǂ̉������ǂ̂悤�ɕω����邩�H���d�v�ł���v�Ƃ������Ƃ�������܂����B
�@�O�ɂ����ẮA��K�ɂ�����b���W���[�X�P�[���ȊO�̉��ɂ�����ٖ������݂̂������܂������A�ٖ������́A���̐�����A�b���W���[�X�P�[����̉��ɑ��Ă����݂��܂��B
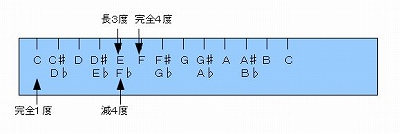
�@�Ⴆ�A���S�S�x�ł���e�̉��́A�d�̉��̔�����ł���܂�����A�d�e�ٖ̈������ƂȂ�܂��B
�@�����x���ŕ\���A�d��́A���R�x�ł���d�������オ�������̂ł��̂ŁA�O��ŏ��������̕ω���K��������ƁA�d��́A�u���R�x�v�Ƃ������ƂɂȂ�킯�ł��B�i�e�����D�W�|�P�|�P�Q�Ɓj
�@
�@ �@�e�����D�W�|�P�|�P�@�@�e�Ƃd��̉����\�L�@
�@�܂��A�t�ɁA���R�x�ł���d�̉��́A�e�̉��̔������ł���܂�����A�e�d�ٖ̈������ƂȂ�܂��B
�@�x���ŕ\���A�e��́A���S�S�x�ł���e�����������������̂ł��̂ŁA����܂����̕ω���K�������āA�e��́A�u���S�x�v�Ƃ������ƂɂȂ�܂��B�i�e�����D�W�|�P�|�Q�Q�Ɓj
�@
�@�@�e�����D�W�|�P�|�Q�@�@E��F��̉����\�L�@
�@�Ƃ������ƂŁA���̗v�̂ōs���A�a�Ƃb�ٖ̈��������A�ȉ��̂悤�ɕ\���܂��B�i�e�����D�W�|�P�|�R�j
�@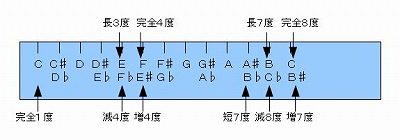
�@�@�e�����D�W�|�P�|�R�@�@B��C�ٖ̈������̉����\�L�@
�W�|�Q�D�d���Əd��
�@���Fig�D�W�|�P�|�R�ɂ����ẮA�b��c�ٖ̈������͏����Ă��Ȃ���Ԃł��B
�@�������A����ɂ��A��͂�ٖ������͑��݂��܂��āA�t���b�g�̂���ɔ������ł���_�u���t���b�g�ŕ\�����u�d���v��A�V���[�v�̂���ɔ�����ł���_�u���V���[�v�ɂ���ĕ\�����u�d���v�����p�����A����ɑΉ����邱�ƂɂȂ�܂��B
�@���Ȃ킿�A�O��̖��̕ω��̕\���A���ڂ��������ƁA�ȉ���Fig�D�W�|�Q�|�P�̂悤�ɂȂ�܂��B
�@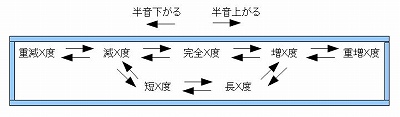
�@�@�e�����D�W�|�Q�|�P�@�@�d���Əd�����܂߂����̕ω��@
�@�Ƃ������ƂŁA��K��ɂ���f�����Ă����ƁA�₽��ƈٖ��������炯�ɂȂ�A���E���t���Ȃ��Ȃ��Ă��܂��̂ł����A�Ƃ肠�����A�b�C�c�C�f�C�`�̉������ɏ������ꂽ���̂��A�ȉ���Fig�D�W�|�Q�|�Q�Ɏ����܂��B�i�_�u���V���[�v�́A�L���������̂ŁA�]�ɂđ�p�����Ă��������܂��B�j
�@�h�_�u���t���b�g�Ȃ�ΕK���u�d���v�Ƃ����킯�ł��Ȃ��h�Ƃ��������Ƃ�����܂�����A��L�̕ω��̐}�����Ȃ���A�\���Ɋ���Ă����Ă��������B�i�b���͏d���P�x�A�f���͏d���T�x�Ƃ��������ƂɂȂ�܂��B�j
�@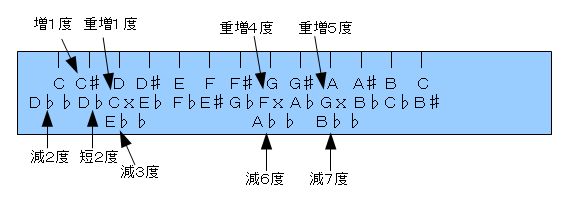
�@�@�e�����D�W�|�Q�|�Q�@�@�_�u���t���b�g�A�_�u���V���[�v���܂߂���K�̐}�@
�W�|�R�D�h�Q���Ԃ̑S���Ɣ����̐��Ŕ��f�h�Ƃ�������
�@����ŁA�قƂ�ǂ̏ꍇ�̂Q���Ԃ̓x���ɂ�鉹���\�L���ł���悤�ɂȂ����͂��ł��B
�@����܂łɂ������܂����悤�ɁA���̂�����̘b�́A���ۂɂ́A�R�[�h�i�a���j�̍\�����̕\�L�Ƃ�������ʂŊ���Ă����Ηǂ��̂ł����A�܂��́A��{���K�Ƃ������ƂŁA�ȉ��̂悤�Ȗ��ɓ����邱�Ƃ���n�߂Ă��ǂ��ł��傤�B
�i�������A�Ⴂ���̂ق��Ɍ������x���̕\�L���\�ł����A�Ƃ肠�����́A����������������̉��܂ł̉����Ƃ��܂��B�j
��P�D�c����Ƃ����ꍇ�A�e�Ƃ̊Ԃ̉����́H
��Q�D�d����Ƃ����ꍇ�A�f�Ƃ̊Ԃ̉����́H
��R�D�c����Ƃ����ꍇ�A�d��Ƃ̊Ԃ̉����́H
��S�D�f����Ƃ����ꍇ�A�f��Ƃ̊Ԃ̉����́H
����
��P�D
�@������̖��ɂ��Ă��A�܂��́A�Q���ԂɑS���Ɣ��������������邩�H���m�F���邱�Ƃ��K�v�Ȃ̂ł����A���̑O�ɁA���́A�u�x���̐����̕����͊ȒP�ɑ{���o����v�Ƃ�������������܂��B
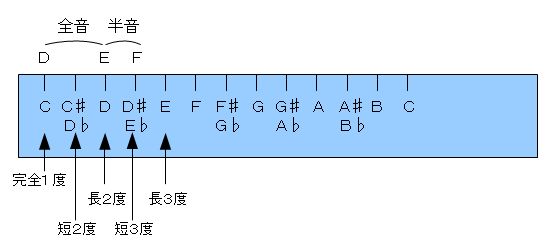
�@��P�́A�c�Ƃe�ł��̂ŁA��ł���c���P�i�P�x�j�Ƃ���A�A���t�@�x�b�g���ɐ����Ă͂߂āA�h�c�i�P�j�˂d�i�Q�j�˂e�i�R�j�h�ƂȂ�܂�����A�e�͂R�x�̉����ł��邱�Ƃ��킩��Ƃ������Ƃł��B�@���Ȃ킿�A�e�́A�u�`�R�x�v�Ƃ������Ƃł��B�i�e�����D�W�|�R�|�P�Q�Ɓj
�@
�@�@�e�����D�W�|�R�|�P�@�@�c�Ƃe�̓x���̐��������@
�@���������āA�u�`�R�x�v�́`�����Ȃ̂��Z�Ȃ̂��H�A�܂��́A���Ȃ̂����Ȃ̂��H�Ƃ��������ƂɂȂ�܂��䂦�A���Ƃ́A�Q���Ԃ̑S���Ɣ����̐����m�F���A��̒�K��̕\�L�ƌ���ׂĂ݂�Ηǂ��킯�ł��B
�@�c�|�S���|�d�|�����|�e�ƂȂ�܂�����A�c�Ƃe�̊Ԃ́A�P�S���{�P�����A�܂�P�S�����ł��B
�@����ɑ�������R�x�͉����ƌ����A��K��̌��_�b���A��P�ł̂c�ɑ�������ƍl����Ηǂ����Ƃ���A�b�̂P�S������͂d��A�v�́A�u�c�ɑ���e�v�́u�b�ɑ���d��v�Ɠ����Ƃ������ƂɂȂ�A�����́A�u�Z�R�x�v�Ƃ������ƂɂȂ�܂��B�i�e�����D�W�|�R�|�Q�Q�Ɓj
�@
�@�@�e�����D�W�|�R�|�Q�@�@��K�ɂĂc�Ƃe�Ƃ̓x����������@
��Q�D
�@��P�Ɠ����悤�ɁA�܂��́A�x���̐����T������B
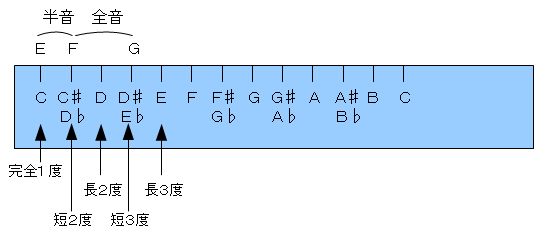
�@�h�d�i�P�j�˂e�i�Q�j�˂f�i�R�j�h�ƂȂ�܂�����A�f�͂R�x�̉����ł��B�@�f�́A�u�`�R�x�v�Ƃ������Ƃł��B�i�e�����D�W�|�R�|�R�Q�Ɓj
�@
�@�@�e�����D�W�|�R�|�R�@�@�d�Ƃf�̓x���̐��������@
�@�����āA������������A�Q���Ԃ̑S���Ɣ����̐����m�F���A��K��̕\�L�ƌ���ׂ܂��B
�@�d�|�����|�e�|�S���|�f�ƂȂ�܂�����A�d�Ƃf�̊Ԃ́A�P�����{�P�S���A�܂�P�S�����ł��B
�@�����Œ��ӂȂ��Ƃ́A������S���Ɣ����̑��v�́A�u�P�S�����v�Ƃ������Ƃł��B�@��P�̂悤�Ɂu�P�S���{�P�����v�ł����Ă��A��Q�̂悤�ɑS���Ɣ����̏������t�ɂȂ��āu�P�����{�P�S���v�ł����Ă��A���v�͂ǂ�����u�P�S�����v�ł��B
�@���Ȃ킿�A�Q�̉��ԂŁA�S���Ɣ����̏o�Ă��鏇�Ԃ́A�x���ɂ͊W�����Ƃ������Ƃł���A����́A������O�Ƃ͌����A���������ȏd�v�����ƂȂ���̂ł��B
�@����āA����ɑ�������R�x�͉����ƌ����A��K��Ō��Ă��A���ǁA��P�Ɠ������ƂŁA�����́A�u�Z�R�x�v�Ƃ������ƂɂȂ�܂��B�i�e�����D�W�|�R�|�S�Q�Ɓj
�@
�@�@�e�����D�W�|�R�|�S�@�@��K�ɂĂd�Ƃf�Ƃ̓x����������@
��R�D
�@����́A�Q���Ԃ��P�S�����ł����Ă��Z�R�x�ɂȂ�Ȃ���ł����āA����܂��d�v�ł��B
�@�܂��́A�ȑO�ɂ��������u���Ƃ��Ɖ��̉����ǂ��ω��������H�v�Ƃ������Ƃ��A�傢�ɊW������̂ł����A�d��ł����炵�āA�����܂ł�����͂d�̉����ω������i�����オ�����j���̂ł��B
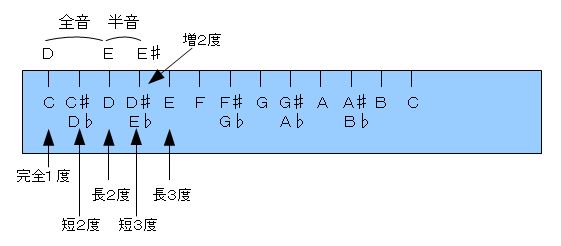
�@����āA���̂悤�ȏꍇ�A�A���t�@�x�b�g�ɂ����ẮA���̕ω��L�����t���Ă�����̂��̂Ƃ݂Ȃ��܂��āA�h�c�i�P�j�˂d�i�Q�j�˂d��i�Q�j�h�ƂȂ�A�d��́u�Q�x�̉����̉����H�v�Ƃ������ƂɂȂ�܂��B
�@
�@�@�e�����D�W�|�R�|�T�@�@�c�Ƃd��̓x���̐��������@
�@�����āA�Q���Ԃ̑S���Ɣ����̐��̊m�F�ƂȂ�܂����A��K��̕\�L�ƌ���ׂ܂��B
�@�c�|�S���|�d�|�����|�d��ƂȂ�܂�����A�c�Ƃd��̊Ԃ��A��̖�Ɠ������u�P�S�����v�ł��B
�@�ł��A�u�`�R�x�v�ł͂Ȃ��A�u�`�Q�x�v�ł��邱�Ƃ��킩���Ă��܂�����A����ɒ��ӂ��Ȃ����K��̓x���ɏƂ炵���킹�Ă݂�킯�ł��B
�@����ƁA���Q�x�̔�����A���Ȃ킿�A�u���Q�x�v�ł���Ƃ������Ƃ��킩��܂��B�i�e�����D�W�|�R�|�U�Q�Ɓj
�@���̂悤�ɁA�P���ɂQ���Ԃ̑S���Ɣ����̐��Ōv��ɂ͒��ӂƂȂ邱�Ƃ�������̂ł��B�@��͂�A�ŏ��ɓx���̐��������߂�ۂɋC��t����ׂ��ƂȂ�ł��傤�B
�@
�@�@�e�����D�W�|�R�|�U�@�@��K�ɂĂc�Ƃd��̓x����������@
��S�D
�@����́A�ӊO�ƌ˘f����������܂���B
�@�ł��A���y���E�̒�K�ł́A���_�͂O�x�ł͂Ȃ��A�P�x�i���S�P�x�j�ł��邱�Ƃ�����x�m�F���Ă���������A�ʂɂ����������Ƃ͂Ȃ��͂��ł��B
�@�܂�����A��͍l�����ɁA�f�i�P�j�˂f��i�P�j�@�ƂȂ�A�f��́u�`�P�x�v�Ƃ������Ƃ��킩��܂��B
�@����́A�f����_�ł�����A�f���u���S�P�x�v�A���̔����オ�f��ł�����A�����́u���P�x�v�ł��B
�@�}�������܂ł��Ȃ��ł��傤�B
�@���̂悤�Ȋ����ŁA�l�X�ȏꍇ�ɂ�����x���W�ł̂�������̖₢�������ō���ăg���C���Ă����Ɨǂ��Ǝv���܂��B
�@�����Ȃ�ɁA���̑��̐F�X�Ȓ��ӓ_�������Ă���ł��傤�B
�@�����āA���̓x���ɂ�鉹���\�L�̊T�O���A������O�̘b�Ɋ�������悤�ɂȂ��Ă���Ǝv���܂��B
�@����́A���������Ƃ��܂߂ẮA��K�̊����}�A�Ȃ�тɒ�K�֗̕��Ȏg�����A�����āA�����\�L�̍��̂܂Ƃ߂ł��B
�@�ˈȉ��A����ɑ���
�i�Q�O�P�O�N�@�S�����j
�����p�I�ɉ��y���_���w�ڂ��i��X��F�x���ɂ�鉹���\�L�̘b�i���̂S�j��
�@�S���Ɋ�惉�C�u�����{����������ŁA���̂������A�b�v���x��Ă��܂��܂������A�S�����^�T��������C�Ɍf�ڂ��ẮA�x���\�L�̘b�̑����ł��B�@�i���āA�������ɂU���ł����A�����ւ�\����܂���I�j
�@�Ƃ͌����A�S���^�T�����Ōf�ڂ���̂́A���p�V�Ă��Ƃꂻ���ȁi�H�j�A�m�f�r�l�Ă֗̕����̋L���䂦�A���Ԃ������Ă����Ə������������A�Ƃ������Ƃ�����̂ł��B
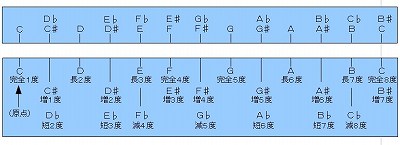
�X�|�P�D�x���̒�K�̊���
�@�܂��́A����܂ł̂܂Ƃ߂Ƃ������ƂŁA���y���E�̒�K�̊����`���ڂ��܂��傤�B
�@�e�����̓x���\�����܂߂āA�ڐ��育�ƂɋL�ڂ������̂��e�����X�|�P�|�P�ł��B
�@�������A�_�u���t���b�g��_�u���V���[�v�̕������Ɋւ��ẮA�S�`���S�`�����Ă��܂��̂ŁA�Ƃ肠�����A��Ɓ�͂P���܂łɂƂǂ߂܂��B�i����ɕt���L�ڂ���_�u���t���b�g�^�d��������̂��̂��ȒP�ɍ��܂��̂ŁA�e���ō���Ă݂Ă���������Ǝv���܂��B�j
�@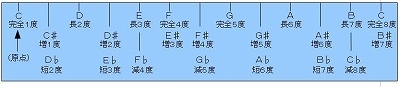
�@ �@�e�����D�X�|�P�|�P�@�@��K�̊����`�@�i�N���b�N�ɂĊg�債�܂��j�@
�X�|�Q�D���A�i���O�x�����������낤�I
�@���āA���̒�K�̊����`�����p����ƁA�̂̎G���̕t�^�I�i�H�j�A���A�i���O�ȁu�x��������v�i�h�X�E �n���~�L�j����邱�Ƃ��ł��܂��B
�@�v�́A�C�ӂ̂Q���Ԃ̓x���������H����u�ɂ��đ{�����Ƃ��ł���֗��ȓ���ł���܂��B
�@�Ƃ������ƂŁA��L�̒�K�̐}�ɉ����A���������ɏ�ɐ܂�Ԃ��悤�Ȍ`�Ŗڐ��蕔���������P���ׂĒu�����}�����܂��B
�@�ȉ��̂e�����X�|�Q�|�P������ł����A������A���߂̃v�����^�[�p���Ƀv�����g�A�E�g���܂��傤�B
�@
�@ �@�e�����D�X�|�Q�|�P�@�@�x��������̐}�@�i�N���b�N�ɂĊg�債�܂��j�@
�@
�@�@�e�����D�X�|�Q�|�Q�@�@���߂̗p���Ƀv�����g�A�E�g����@
�@�����āA�㉺�Q��̒�K�̐}���ɁA�A�E�g���C���ɉ����Đ��āA��K�̐}�̕����݂̂�蔲���܂��B�i�e�����D�X�|�Q�|�R �Q�Ɓj
�@
�@�@�e�����D�X�|�Q�|�R�@�@�O�`�ɉ����Đ蔲���@
�@���̂悤�Ȃ��ƂŁA�蔲���ꂽ�Q��́i���̉������H�j��K�̐}���o���邱�ƂɂȂ�܂��B
�@
�@�@�e�����D�X�|�Q�|�S�@�@�蔲���ꂽ��K�̐}�@
�@�ȏ�A�܂��́A���������ł��B
�@������ǂ̂悤�Ɏg�����H�́A����ɂĐ����������܂��傤�I
�@�ˈȉ��A����ɑ���
�@
�i�Q�O�P�O�N�@�T�����j
�����p�I�ɉ��y���_���w�ڂ��i��P�O��F�x���ɂ�鉹���\�L�̘b�i���̂T�j��
�@���悢��A�O�������u�x��������v�̎g�����ł��B
�@���A�i���O�Ȃ���A����Ȃɕ֗��Ȃ��̂͂���܂���B�i�܂��A�x���ɂ��ė�������A����Ȃ��̂��g��Ȃ��Ă��ǂ��킯�ł����E�E�i�j�j
�P�O�|�P�D�Q�̒�K����ׂăX���C�h
�@�܂��́A�ȉ��̂e�����D�P�O�|�P�|�P�̂悤�ɁA�蔲�����Q��̒�K���A���ꂼ��̖ڐ��蕔���𖧒�������悤�ɂ��ĕ��s�ɕ��ׂ܂��B
�@����ɂ����āA�㉺�̕����������Ă��炵�Ēu���Ă���̂́A�������̒�K�����ɑ��āA�㔼���̕��������E�ɃX���C�h�����Ďg������ł��I
�@
�@�@�e�����D�P�O�|�P�|�P�@�@�Q��̒�K�𖧒������ĕ��ׂ�@
�P�O�|�Q�D���ɂĎ��H�I
�@�ł́A�R�����̋L���ɂď����������l�^�ɁA���������g���Ă݂܂��傤�I
��P�D�c����Ƃ����ꍇ�A�e�Ƃ̊Ԃ̉����́H
�@�R�����ɂď�������v�Z�i�H�j�ł̓x���̋��ߕ��ɂ����ẮA�u�܂��́A�Q���Ԃ��A���t�@�x�b�g���ɂĊ��肷��A�x���̐����̕����͂킩��v�Ƃ������Ƃ������܂����B
�@����́A�u�x��������v�ɂ����Ă��A�c�O�Ȃ���i�H�j�����ŁA�x���̐����̕����́A�ÎZ�I�ɏo���Ă����K�v������܂��B�@�Ƃ͌����A�A���t�@�x�b�g���ɂĐ����邾���ł�����A�ȒP�Ȃ��Ƃł��傤�B
�@�R�����̋L���Ɠ������A�ȉ��̂e�����P�O-�Q-�P�̂悤�ɂȂ�܂��䂦�A�x���̐����͂R�ŁA���߂���̂́u�`�R�x�v�Ƃ������Ƃ������邱�ƂɂȂ�܂��B
�@
�@
�@�@�e�����D�P�O�|�Q�|�P�@�@�c�Ƃe�̓x���̐��������@
�@���ɁA���悢��A������̏o�Ԃł��B
�@�Q��̒�K�̂����A�㕔�̒�K���X���C�h�����A�����̒�K�̂b�i���_�j�̈ʒu�ɁA�㕔�̖ڐ���̂c������悤�ɂ��܂��B
�@�����āA���̎��A�㕔�̖ڐ��肪�e�̈ʒu�̐^���́A�����̒�K��ɂāA�`�R�x�ɂȂ��Ă���L�ڂ�T���Ηǂ��̂ł��B
�@�R�x���t�����̂́A�Z�R�x�݂̂ł��B�@�܂�A�����́u�Z�R�x�v�Ƃ����킯�ł��B�i�e�����P�O-�Q-�Q�Q�Ɓj
�@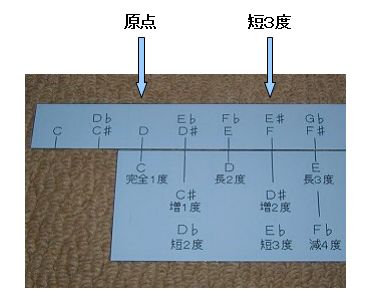
�@�@�e�����D�P�O�|�Q�|�Q�@�@�������ł̂c�Ƃe�̓x���@
��Q�D�d����Ƃ����ꍇ�A�f�Ƃ̊Ԃ̉����́H
�@��P�Ɠ��l�ɂ��āA�܂��́A�x���̐����͂R�ł��B
�@��K�̏㕔���X���C�h�����A�����̌��_�ɂd�����킹��A�f�̈ʒu�̐^���łR�x�̂��̂́A�u�Z�R�x�v�ł��B�i�e�����P�O-�Q-�R�Q�Ɓj
�@����āA�����́u�Z�R�x�v�ł���܂��B
�@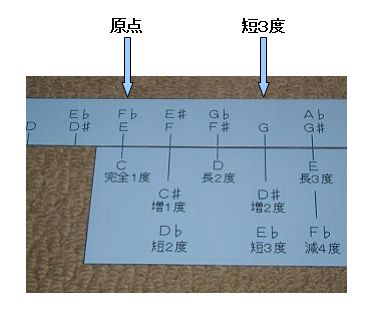
�@�@�e�����D�P�O�|�Q�|�R�@�@�������ł̂d�Ƃf�̓x���@
��R�D�c����Ƃ����ꍇ�A�d��Ƃ̊Ԃ̉����́H
�@�x���̐����͂Q�ł��B
�@��K���X���C�h�����A���_�ɂc�����킹��A�d��̈ʒu�̐^���łQ�x�̂��̂́A�u���Q�x�v�ł��B�i�e�����P�O-�Q-�S�Q�Ɓj
�@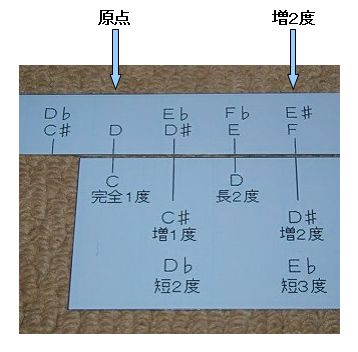
�@�@�e�����D�P�O�|�Q�|�S�@�@�������ł̂c�Ƃd��̓x���@
��S�D�f����Ƃ����ꍇ�A�f��Ƃ̊Ԃ̉����́H
�@�x���̐����͂P�ł��B
�@��K���X���C�h�����A���_�ɂf�����킹��A�f��̈ʒu�̐^���łP�x�̂��̂́A�u���P�x�v�ł��B�i�e�����P�O-�Q-�T�Q�Ɓj
�@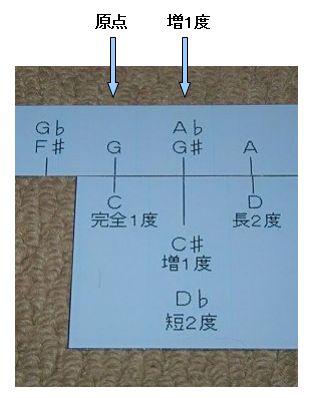
�@�@�e�����D�P�O�|�Q�|�T�@�@�������ł̂f�Ƃf��̓x���@
�@�Ƃ����킯�ŁA���́u�x��������v�͂������ł��傤�B
�@�x���̊T�O�Ɋ���Ă��܂��A���̂悤�Ȃ��̂��g���K�v�͂Ȃ��̂ł����A�܂�����Ă��Ȃ������́A�x���̍l�����𗝉������ł��A�֗��Ȃ��̂ɂȂ邩�Ǝv���܂��B
�@�x�������߂�\�t�g�Ȃ�web��ɂ͑��݂��܂����A���̂悤�Ȃ��̂��g�������ł́A�����ŗ������ɂ����ł��̂ŁA����ȃv���~�e�B�u�ȑ㕨�ł��A�����������ɗ������肵�܂��B
�@����́A�������������A����̊��̎g�������܂߁A�x���Ɋւ���⑫�����������āA���̍����I���ɂ������Ǝv���܂��B
�@�ˈȉ��A����ɑ���























